This paper introduces an algorithm for automatic simplification of articulated body dynamics: an animator specifies the number of joints that should be simulated in the articulated body, and the algorithm automatically determines which joints should be simulated in order to best approximate the articulated body motion. The other joints are rigidified.

Depending on the amount of simplification specified by the animator, this algorithm potentially allows for a significant speed-up compared to traditional linear time forward dynamics algorithms.



Progressive dynamics

The following figure shows the progressive simplification of the motion of a pendulum. The adaptive dynamics algorithm allows for a graceful simplification of the pendulum motion when 300, 100, 50, 20 and finally 1 joints are allowed to be simultaneously active.
This video shows the progressive simplification.



Adaptive refinement

At any time, the algorithm predicts which joints contribute most to the articulated body motion, and simulates those joints only. The set of simulated joints is determined based on the current state of the articulated body, the external forces applied to it, the active joint forces, and customizable motion metrics.

The next figure shows an example of the adaptive selection of the set of active joints: (a) one of the links of a 50-link pendulum is attached to a point in the environment through a spring; (b) equilibrium state when 50 joints are active; (c) equilibrium state when 5 joints are active, without adaptive determination of the active joints (breadth-first selection); (d) equilibrium state when 5 joints are active, with adaptive determination of the active joints by the adaptive dynamics algorithm.


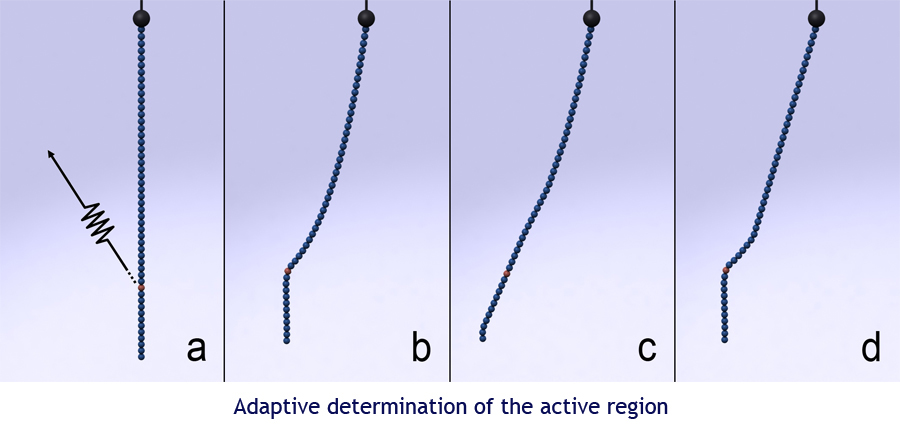
Click here to see a video showing the adaptive determination.



Time-dependent simplification

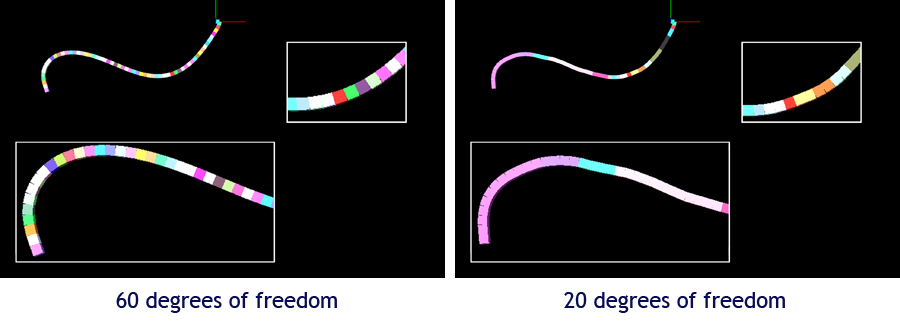
To help obtain a high-quality approximation of the articulated body motion, the set of active joints evolves over time. The following figure shows two snapshots of the simulation of a 60-joint pendulum. One color is used per rigid (or rigidified) sub-assembly. The left image shows the state of the pendulum, at a given instant, when all joints are simulated. The right image shows the state of the pendulum, at the same instant, when 20 joints only have been allowed to be simultaneously active throughout the simulation.




The next figure compares the pendulum states at a later instant, when the motion of the pendulum is mainly concentrated in its lower part. The adaptive algorithm rigidifies the upper part to maintain the higher frequency motion in the lower part.



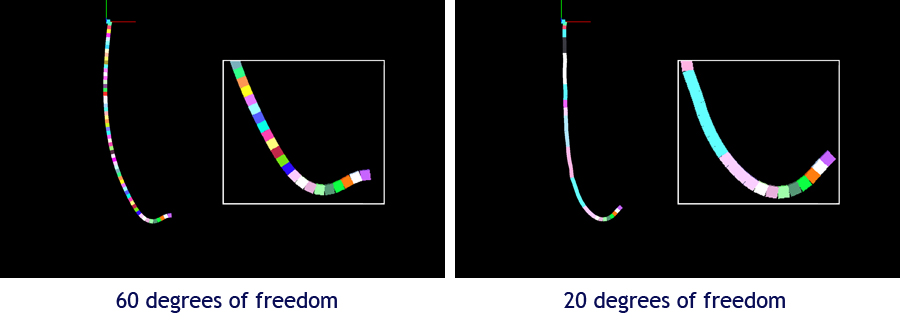
The time-dependent selection of the set of active joints is best viewed in this video (DivX).

An application

The following figure shows a complex scene, where 200 human characters, represented by 17,800 rigid bodies and 19,000 degrees of freedom, are suddenly pushed away from the camera due to applied forces. The adaptive dynamics algorithm allows an animator to progressively reduce the number of simulated joints in the characters as their distance to the camera increases, in order to improve the efficiency of the dynamics simulation.

This video describes the "making of" of this test application.

The paper describes the algorithm, and suggests some applications and future research directions, such as view-dependent articulated body dynamics, perceptually-based simplification of articulated body dynamics, adaptive collision detection and response, and articulated body control simplification.



Implementation

An implementation sketch discusses several implementation details.

Links