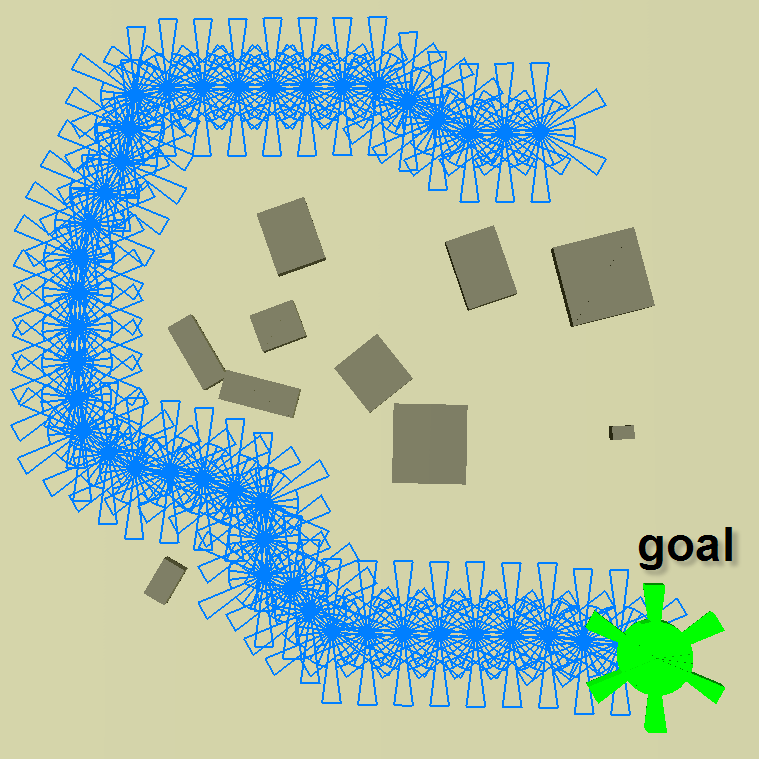
Feedback
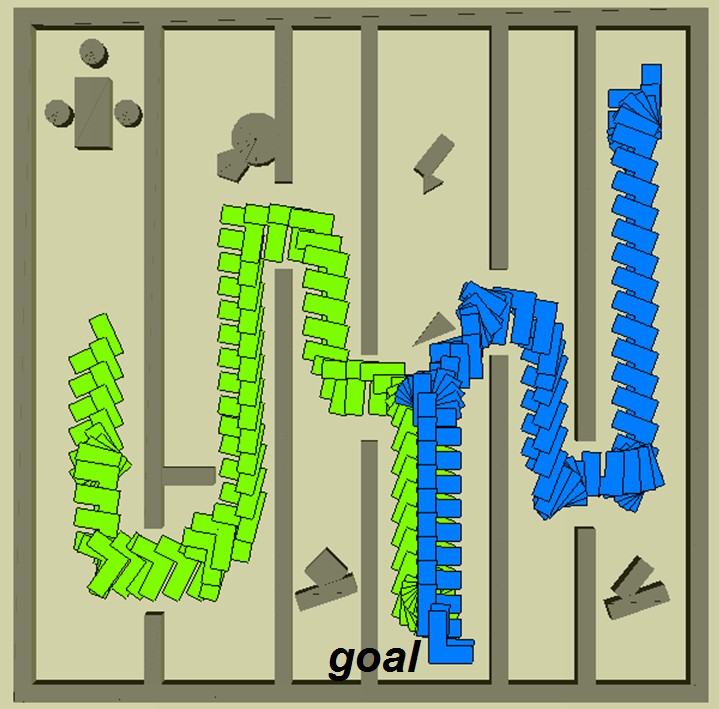
planning for a translating Gear-shaped
robot with 2 degrees of freedom (DOF)

Approximate
cell
decomposition in the robot's configuration space
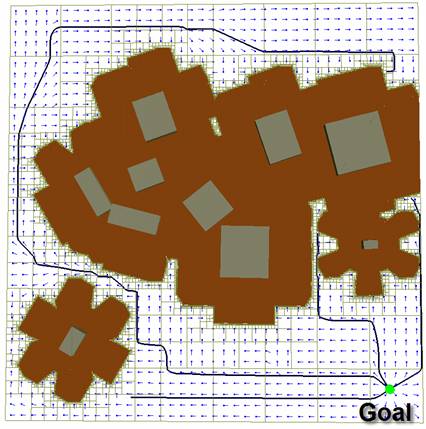
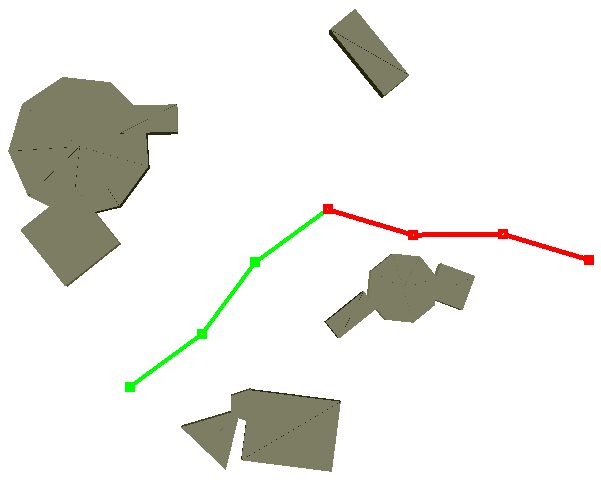
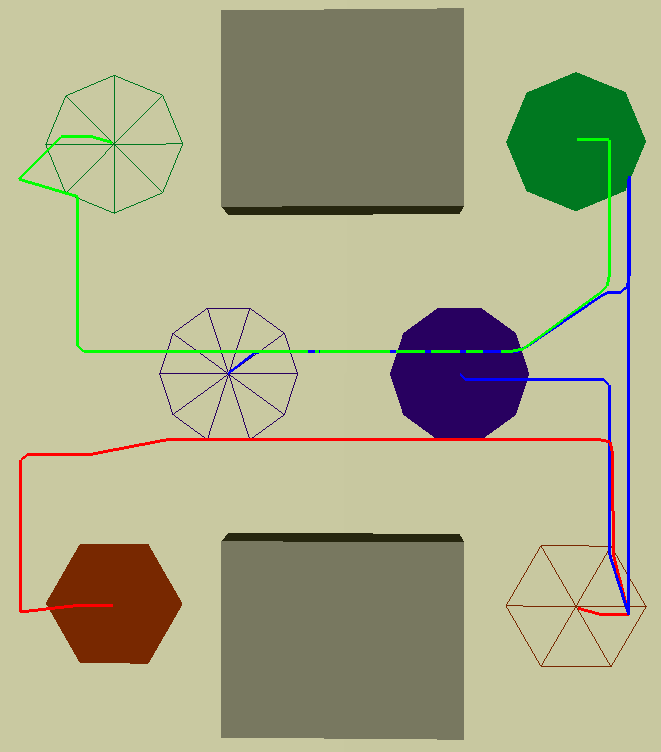
A vector
field is
computed in the robot's free space. All integral curves over the vector
field
are guaranteed to converge to the goal.