Constrained Motion Interpolation with Distance Constraints

Constrained Motion Interpolation
with Distance Constraints

Liangjun Zhang, Dinesh Manocha
GAMMA Group

University of North Carolina at Chapel Hill

The Seventh International Workshop on the Algorithmic Foundations of Robotics (WAFR), 2008, Paper

Introduction

We address the problem of computing a collision-free interpolating motion between two free-space configurations. The goal is to compute a trajectory that is less likely to intersect with any obstacles in the configuration space (C-space).

The main motivation is the local planning step in sample-based planners, which attempts to connect two nearby free-space samples with a collision-free path. The performance of sample-based planners may degrade when the free space has narrow passages. Most of the prior work in improving the performance of planners has focused on increasing the probability of sampling in these regions. Instead, we focus on the local planning step, which computes an interpolating path and checks that path for collisions with the obstacles.

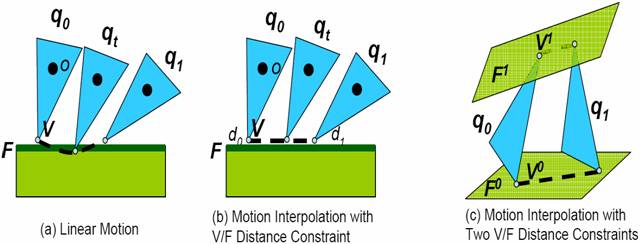
Fig. 1: Motion Interpolation between two configurations q₀ and q₁ (a) There is collision at the intermediate configuration q_t if we use a linear interpolation; (b) Using our constrained interpolation algorithm, we obtain a collision-free trajectory for this case. (c) We take into account multiple closest feature pairs (V⁰, F⁰) and (V¹, F¹) in this case) at the two configurations, and guarantee no collisions among these feature pairs along the trajectory. The use of multiple feature pairs increases the probability of finding a collision-free path for the local planner.

Distance Constraints

If the sign of the distance function for a feature pair (V, F), (F, V) or (E,E) between the robot and obstacles does not change when the robot moves, then there is no collision in this feature pair.

In order to guarantee that the sign of the distance function does not change, a simple but sufficient way is to perform a linear interpolation on the signed distances if initially both d₀ and d₁ have the same sign. Other more complex polynomial interpolation functions can have been used.

Multiple distance constraints are considered in our formulation. We compute the locally closest feature pairs between the robot and obstacles (Fig. 1(c)). We derive closed forms for our constrained interpolation which can consider up to three locally closest feature pairs. By taking into account multiple constraints, the resulting interpolating motion conforms better to the local geometry of c-obstacles in the configuration space.

Motion Interpolation with Distance Constraints

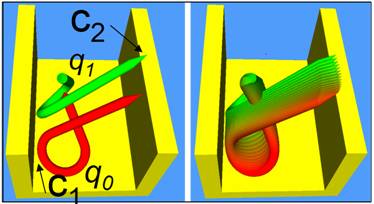
Two distance constraints

Three distance constraints.

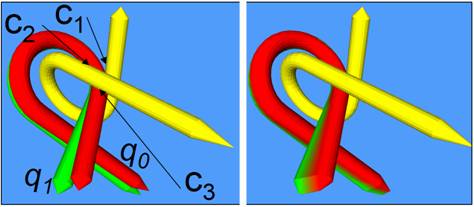
A video clip compares different motion interoplation schemes.

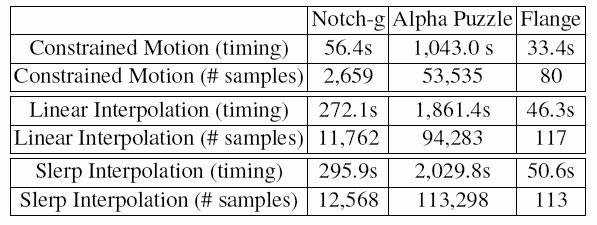
Local Planning in Sample-based Planners

The following video clips highligths the collision-free paths computed using our new constrained motion interpolation algorithm. We integrate our local planner into a retraction-based RRT planner and compare its performance with the original planner that used straight-line linear interpolation algorithm. We report the time taken and the samples generated by our new planner as compared to the earlier planner.